Answer: Option C
C) No solution
Explanation:
To graph both lines identify the cut points with the axes
For
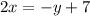
The intersection with the x axis is:

The intersection with the y axis is:
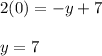
Draw a line that cuts the y-axis in 7 and the x-axis in 3.5
For
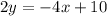
The intersection with the x axis is:
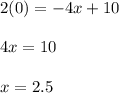
The intersection with the y axis is:
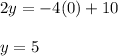
Draw a line that cuts the y-axis in 5 and the x-axis in 2.5
The intersection of both lines will be the solution of the system. Observe the attached image
The lines are parallel, so they never intercept. Therefore the system has no solution