Answer:
The constant of proportionality is 5.
Explanation:
If the quantity q varies inversely with the square of m and directly with the product of r and x, then the variation equation is
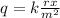
When q=2.5, m= 4 and the
product of rx = 8.
We plug in this values to get;
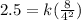
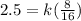
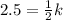
Multiply both sides by 2
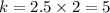
The constant of proportionality is 5.