The correct option is c.
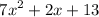 is equal to
is equal to
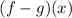 .
.
To find the expression for
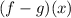 , we need to subtract the function
, we need to subtract the function
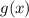 from
from
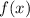 . Let's do this step by step.
. Let's do this step by step.
The functions
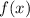 and
and
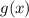 are given as:
are given as:
![\[ f(x) = 7x^2 + 4 \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/s9092mu4kqdj5ztr3igffhwfq53d31ep5a.png)
![\[ g(x) = 2x + 9 \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/dn9k3ukyn6xewo866r167oxnrs4hmdgf7y.png)
Now,
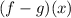 is defined as:
is defined as:
![\[ (f-g)(x) = f(x) - g(x) \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/hf0215aamalx9eovely7ijvcmyo20l2d6a.png)
Substituting the given functions into this, we get:
![\[ (f-g)(x) = (7x^2 + 4) - (2x + 9) \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/yr2womnev9bxjjbwogql2tqe3n3zhwr2me.png)
Now, let's simplify this expression:
![\[ (f-g)(x) = 7x^2 + 4 - 2x - 9 \]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/i8o3ic5dzlzjgb579ca0dxeoeb9hlxn0da.png)
To simplify the expression
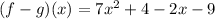 , you can simply subtract
, you can simply subtract
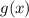 from
from
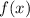 :
:
![\[(f-g)(x) = f(x) - g(x) = (7x^2 + 4) - (-2x - 9)\]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/s49gyjpi6b3m927gaqmg6n5cj4axcipvww.png)
Now, you can simplify further by distributing the negative sign on
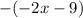 to make it positive:
to make it positive:
![\[(f-g)(x) = 7x^2 + 4 + (2x + 9)\]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/gbne6pgafsazyyfcgpk5cdfs62bum0xyr9.png)
Now, combine like terms:
![\[(f-g)(x) = 7x^2 + 2x + 13\]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/4h3yorpgds5pm2q5s2kdmmrlpvqwohxiqw.png)
So,
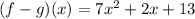 .
.
Therefore, the answer is
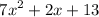 .
.