Answer:
Option D will be the answer.
Explanation:
y intercept form of a line is represented by y = mx + c
Where m = slope of the line and c = y- intercept of the line.
A line passing through two points (2, 5) and ( 6, 7) has the slope
m =

=
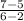
=
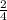
=

Equation will be y =
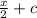
This line passes through (2, 5)
5 =
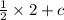
c = 5 - 1
c = 4
And the equation will be y =
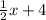
Since a point (k 11) passes through the line then we will plug in these values in the equation to find the value of k.
11 =
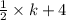
11 - 4 =
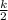
7 =
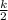
k = 2×7
= 14
Option D will be the answer.