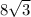Answer:
Explanation:
In a 45°, 45°, 90° triangle, Both legs are equal and the hypotenuse is the leg lengths multiplied by the square root of 2.
- Given a triangle with a 45° and 90° angle, the other angle must also be 45°.
- In any of these triangles, the hypotenuse is
 times the side length. You can also find the side length by dividing the hypotenuse by
times the side length. You can also find the side length by dividing the hypotenuse by
 .
.
- You can also use this to determine both the legs are the same length. This works the other way too, if both legs are the same length (indicated by a line draw through both sides) the angles opposite to the same length legs are 45°.
In a 30°, 60°, 90° triangle, The hypotenuse is twice the length of the shortest side (the one opposite the 30° angle) and the other leg (the one opposite the 60° angle) is the short leg times

- If a triangle has two angles out of 30°, 60°, 90°, the last angle must be the only other different angle (because they have to sum to 180)
1. Your answer to the first problem is correct.
2. Because there is a line through two of the sides, they are the same length, and the hypotenuse is
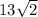 , the sides are both of length
, the sides are both of length
 or 13.
or 13.
3. We can see that there is a 90° angle (from the square in the corner) and a 45° angle. This means that the two legs have equal length. One leg is
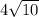 so the other is the same. The hypotenuse is
so the other is the same. The hypotenuse is
 , or
, or
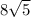
4. The hypotenuse is twice the length opposite the 30° angle (9), so it's length is 18. The last angle must be 60° and the side opposite the 60° must be
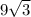
5. There are two 45, 45, 90 triangle that make up a square. The hypotenuse of both of these is 24, meaning the side lengths are
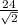 , or, (rationalized),
, or, (rationalized),
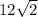
6. 30 60 90 triangle, short side is
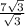 or 7 and hypotenuse is twice that length, so it is 14.
or 7 and hypotenuse is twice that length, so it is 14.
7. 45 45 90 triangle, hypotenuse is 7 so lengths are
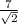 or
or
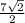
8. 30 60 90 triangle, longer leg is 18, shorter leg is
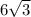 , hypotenuse is
, hypotenuse is
 ,
,
9. 45 45 90 triangle, hypotenuse of
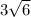 , side lengths of
, side lengths of

10. 30 60 90, hypotenuse of 28, shorter leg 14, longer leg
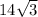
11. 30 60 90, hypotenuse 15, shorter side
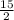 , longer leg
, longer leg
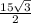
12. Two 30 60 90 triangles, hypotenuses of 16, shorter legs of 8 and longer legs of