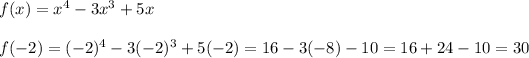Question

Let f(x)=x^4-3x^3+5x use synthetic substitution to find f(-2)

Answer 1

f(-2) = 30

Explanation:

`f(x)=x^4-3x^3+5x=1x^4-3x^3+0x^2+5x+0`

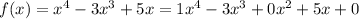
The Remainder Theorem states that when we divide a polynomial f(x)

by x − a the remainder R equals f(a).

a = -2

Syntetic substitution.

1. Write only the coefficients of x in the dividend inside an upside-down division symbol.

`\underline{\begin{array}ccccccc\ &1&-3&0&5&0\\\ \end{array}}`

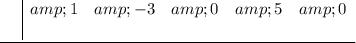
2. Put the divisor at the left.

`\underline{\begin{array}c-2&1&-3&0&5&0\\\ \end{array}}`

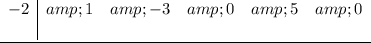
3. Drop the first coefficient of the dividend below the division symbol.

`\underline{\begin{array}ccccccc-2&1&-3&0&5&0\\\ \end{array}}\\\begin{array}{ccccccccc}\ \ \ \ &1\end{array}`

4. Multiply the drop-down by the divisor, and put the result in the next column.

`\underline{\begin{array}ccccccc-2&1&-3&0&5&0\\\ &&-2\end{array}}\\\begin{array}{ccccccccc}\ \ \ \ &1\end{array}`

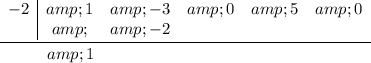
5. Add down the column.

`\underline{\begin{array}ccccccc-2&1&-3&0&5&0\\\ &&-2\end{array}}\\\begin{array}{ccccccccc}\ \ \ \ &1&-5\end{array}`

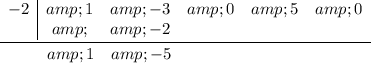
6. Repeat 4 and 5 until you can go no farther

`\underline{\begin{array}c-2&1&-3&0&5&0\\\ &&-2&10&-20&30\end{array}}\\\begin{array}{ccccccccc}\ \ \ \ &1&-5&10&-15&30\end{array}`

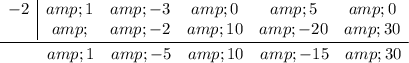
The remainder is 30, so f(-2) = 30.

Check:

`f(x)=x^4-3x^3+5x\\\\f(-2)=(-2)^4-3(-2)^3+5(-2)=16-3(-8)-10=16+24-10=30`