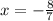Question

Which value of x satisfies both -9x + 4y = 8 and -3x − y = 4 given the same value of y?

A-1/7
B-7/9
C-8/7
D-9
E-4/3

Answer 1

Answer: Option C

C-8/7

Explanation:

We have the following equations

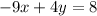`-9x + 4y = 8` and
`-3x - y = 4`

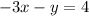
We want to find a value of x that satisfies both equations and obtains the same value of y.

To find the value of x, clear the value of y in both equations

`-9x + 4y = 8\\\\-9x + 4y -8 = 0\\\\-9x -8 = -4y\\\\y = (9)/(4)x +2`

------------------------------

`-3x - y = 4\\\\\-3x -y - 4 = 0\\\\y = -3x -4`

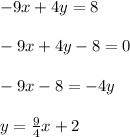
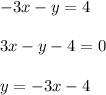
Now solve both equations and solve for x.

`(9)/(4)x +2 = -3x -4\\\\(21)/(4)x = -4-2\\\\(21)/(4)x = -6\\\\21x = -24\\\\x = -(24)/(21)\\\\x = -(8)/(7)`

The answer is
`x = -(8)/(7)`

Answer 2

C

Explanation:

Since y will have same value, y doesn't really matter. Thus,

We can solve for y in the 2nd equation as:

-3x - y = 4

-3x - 4 = y

Now we can plug it into the first and solve for x:

-9x + 4y = 8

-9x + 4(-3x - 4) = 8

-9x - 12x - 16 = 8

-21x = 8 + 16

-21x = 24

x = 24/-21

x = -8/7

Correct answer is C.