Question

The weight of strawberries follows a normal distribution with a mean weight of 12 grams and a standard deviation of 2.5 grams. If a strawberry is randomly selected, what is the probability that the strawberry weighs less than 9 grams?

Answer 1

.2119 is the answer

Explanation:

hope this helps

Answer 2

Answer: 0.1151

Explanation:

Given : The weight of strawberries follows a normal distribution with a mean weight of 12 grams and a standard deviation of 2.5 grams.

i.e.
`\mu=12\ ;\ \sigma=2.5`

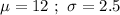
Let x be a random variable that represents the weight of strawberries.

For z-test , we need to find the z-score :-

`z=(x-\mu)/(\sigma)`

For x= 9 , we have

`z=(9-12)/(2.5)=-1.2`

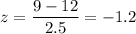
By using the standard normal distribution table , the probability that the strawberry weighs less than 9 grams is given by :-

`P(x<9)=P(z<-1.2)=0.1150697\approx0.1151`

Hence, the probability that the strawberry weighs less than 9 grams = 0.1151