Question

Suppose that there are two types of tickets to a show: advance and same-day. Advance tickets cost $35 and same-day tickets cost $15. For one performance, there were 60

tickets sold in all, and the total amount paid for them was $1300. How many tickets of each type were sold?

Answer 1

26 of each

Explanation:

To solve write this as an equation (35x)+(15x)=1300

Answer 2

For this case we have:

x: Variable representing the types of advance input

y: Variable representing the same-day entry types

We have according to the cost:

`35x + 15y=1300`

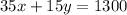
According to the number of tickets:

`x + y = 60`

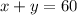
We have a system of two equations with two unknowns:

`35x + 15y = 1300\\x + y = 60`

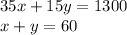
We multiply the second equation by -35:

`35x + 15y = 1300\\-35x-35y = -2100`

We add:

`-20y = -800\\y = \frac {800} {20}\\y = 40.`

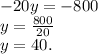
Thus, 40 same-day tickets were sold.

`x + 40 = 60\\x = 60-40\\x = 20`

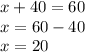
20 advance tickets were sold

Answer:

20 advance

40 same-day