Question

Use the equation to answer the following question y=(x-3(x+2)/(x+4)(x-4)(x+2)

a. Find all points of discontinuity
b. Determine whether each point is removable(hole) or non-removable (vertical asymptote)
c.find the equation of the horizontal and vertical asymptotes for the rational function if any

Answer 1

See below

Explanation:

The given rational function is;

`y=((x-3)(x+2))/((x+4)(x-4)(x+2))`

The given function is not continuous where the denominator is equal to zero.

`(x+4)(x-4)(x+2)=0`

The function is discontinuous at
`x=-4,x=4,x=-2`

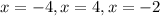
b) The point at x=-2 is a removable discontinuity(hole) because (x+2) is common to both the numerator and the denominator.

The point at x=-4 and x=4 are non-removable discontinuities(vertical asymptotes)

c) The equation of the vertical asymptotes are x=-4 and x=4

To find the equation of the horizontal asymptote, we take limit to infinity.

`\lim_(x\to \infty)((x-3)(x+2))/((x+4)(x-4)(x+2))=0`

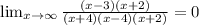
The horizontal asymptote is y=0