ANSWER
A) 9.4 * 10^-8, 9.25 * 10^-6, 2.5 * 10^3, 7* 10^3
EXPLANATION
The numbers are given in standard form.
The first criteria we will use to order them is the exponents.
The bigger the exponents the bigger the number.
The second criteria is that, if the exponents of any two numbers are the same, then we use the numbers multiplying the powers of 10 to order.
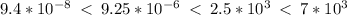
The correct choice is A.