Question

Assume 5000 is deposit in an account that pays 6% annual interest how much more would be in the account after 25 years if it were compounded monthly rather then quarterly

Answer 1

$164.62

Explanation:

Answer 2

`\$164.62`

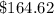
Explanation:

we know that

The compound interest formula is equal to

`A=P(1+(r)/(n))^(nt)`

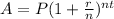
where

A is the Final Investment Value

P is the Principal amount of money to be invested

r is the rate of interest in decimal

t is Number of Time Periods

n is the number of times interest is compounded per year

case A) compounded monthly

in this problem we have

`t=25\ years\\ P=\$5,000\\ r=0.06\\n=12`

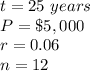
substitute in the formula above

`A=\$5,000(1+(0.06)/(12))^(12*25)=\$22,324.85`

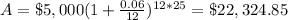
case B) compounded quarterly

in this problem we have

`t=25\ years\\ P=\$5,000\\ r=0.06\\n=4`

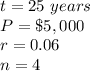
substitute in the formula above

`A=\$5,000(1+(0.06)/(4))^(4*25)=\$22,160.23`

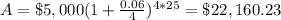
Find the difference

`\$22,324.85-\$22,160.23=\$164.62`