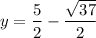Answer:
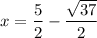 and
and
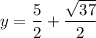
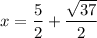 and
and
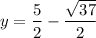
Explanation:
Let the numbers be x and y.
We now have a system of equations.
x + y = 5
xy = -3
Solve the second equation for x.
x = -3/y
Now substitute x in the first equation with -3/y.
-3/y + y = 5
Multiply both sides by y.
-3 + y^2 = 5y
y^2 - 5y - 3 = 0
Use the quadratic formula to solve for y.
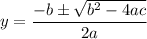

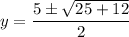

 or
or
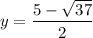
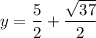 or
or
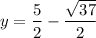
We get 2 solutions for y. Now for each solution for y, we need to find a corresponding solution for x.
Solve the first equation for x.
x + y = 5
x = 5 - y
Substitute each y value to find the corresponding x value.
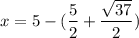
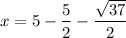
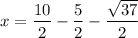
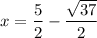
This give one solution as:
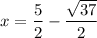 and
and
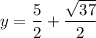
Now we substitute the other y value to find the other x value.
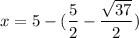
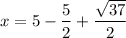
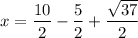
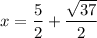
This give the second solution as:
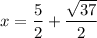 and
and