The inscribed angle theorem says that
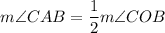
Triangle AOC is isosceles because both AO and CO are radii of the circle and have the same length. This means angles CAO and ACO have the same measure and are congruent.
Angles ACO and COD are congruent because they form an alternating interior pair between the parallel lines AC and OD.
Taking all these facts together, we have
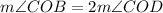
and since angle COB is made up of angles COD and DOB, these angles must be congruent, and so the arcs they subtend (CD and DB, respectively) must also congruent.