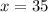Question

If cos x = sin(20 + x)° and 0° < x < 90°, the value of x is

Answer 1

x=35

Explanation:

Answer 2

x=35°

EXPLANATION

We want to find the value of x, when

`\cos(x) = \sin(20 + x) \degree`

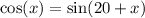
and 0°<x<90°

Recall that the sine and cosine are complementary trigonometric ratios.

Hence cos x = sin (90-x)

Our equation now, becomes;

`\sin(90 - x) \degree= \sin(20 + x) \degree`

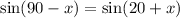
We now equate the argument to get,

`90 - x=20 + x`

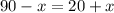
Group similar terms to obtain:

`90 - 20 = x + x`

`70 = 2x`

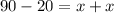
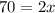
This implies that,

`x = 35 \degree`