Question

Please help! just q4 and q5 thank you

Answer 1

First exercise

Given

`(3x+1)/(x+4)=(2)/(3)`

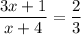
We can cross multiply this equation to get

`3(3x+1)=2(x+4)`

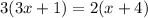
Expand both terms:

`9x+3=2x+8`

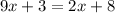
Subtract 2x from both sides:

`7x+3=8`

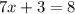
Subtract 3 from both sides:

`7x=5`

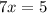
Divide both sides by 7:

`x=(5)/(7)`

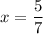
Second exercise

Let
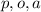`p,o,a` be the number of pine, oath and ash trees. We are given:

`\begin{cases}(p)/(o) = (5)/(8) \iff p = (5o)/(8)\\(o)/(a) = (2)/(3) \iff o=(2a)/(3)\\p+o+a=300\end{cases}`

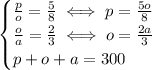
We can substitute the expression for p of the first equation in the last equation to get

`p+o+a=300\iff (5o)/(8)+o+a=300 \iff (13)/(8)o+a=300`

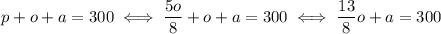
Now we use the second equation, to express o in terms of a:

`(13)/(8)o+a=300 \iff (13)/(8)\cdot (2)/(3)a+a=300 \iff (25)/(12)a = 300 \iff a = 300\cdot (12)/(25) = 144`