Question

Tammy is playing a game where she is tryipg to roll a three with a standard die. If she gets a three in any of her first 4 rolls, she wins; otherwise she loses. What is the probability that Tammy wins the game? Round your answer to the nearest tenth of a percent.

Answer 1

We can partition the events as follows:

`P(\text{win}) = P(\text{win at round 1})+P(\text{win at round 2})+P(\text{win at round 3})+P(\text{win at round 4})`

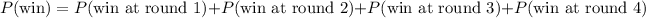
Let's compute each term.

Winning at round 1

To win with the first die, Tammy must roll a 3. This happens with probability 1/6. So, we have

`P(\text{win at round 1})=(1)/(6)`

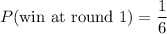
Winning at round 2

To win with the second die, Tammy must not roll a 3 with the first roll (probability 5/6), and then roll a 3 with the second roll (probability 1/6). So, we have

`P(\text{win at round 2})=(5)/(6)\cdot(1)/(6)`

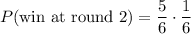
Winning at round 3

To win with the third die, Tammy must not roll a 3 with the first two rolls (probability 5/6), and then roll a 3 with the third roll (probability 1/6). So, we have

`P(\text{win at round 3})=(5)/(6)\cdot(5)/(6)\cdot(1)/(6)`

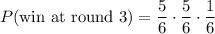
Winning at round 4

To win with the fourth die, Tammy must not roll a 3 with the first three rolls (probability 5/6), and then roll a 3 with the fourth roll (probability 1/6). So, we have

`P(\text{win at round 4})=(5)/(6)\cdot(5)/(6)\cdot(5)/(6)\cdot(1)/(6)`

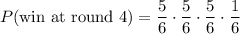
So, we have

`\displaystyle P(\text{win}) = (1)/(6)+(1)/(6)\cdot(5)/(6)+(1)/(6)\cdot\left((5)/(6)\right)^2+(1)/(6)\cdot\left((5)/(6)\right)^3 = (1)/(6)\sum_(i=0)^3 \left((5)/(6)\right)^i\approx 0.5`

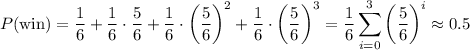
Note

You can do this exercise more quickly by observing

`P(\text{win}) = 1-P(\text{lose})`

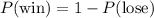
And you lose if you never roll a 3 in 4 rolls (each failure has a probability of 5/6). In fact, you have

`1-\left((5)/(6)\right)^4 \approx 0.5`