Hello!
The answer is:

Why?
To solve this problem, first we need to derivate the given function, and then, evaluate the derivated function with x equal to 2.
The given function is:
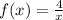
It's a quotient, so, we need to use the following formula to derivate it:
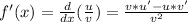
Then, of the given function we have that:
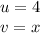
So, derivating we have:
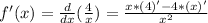
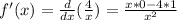
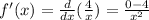

Hence,

Now, evaluating with x equal to 2, we have:
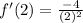
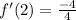

Therefore, the answer is:

Have a nice day!