Question

A projectile is shot into the air following the path, h(x) = -3x2 + 30x + 300. What will its maximum height reach?

Answer 1

375 units

Explanation:

"What will its maximum height be?"

The given equation, h(x) = -3x^2 + 30x + 300, is a quadratic with coefficients a = -3, b = 30 and c = 300.

The axis of symmetry of this parabola will go thru the max ht. The equation of the axis of symmetry is

x = -b / (2a)

In this particular case, the axis of symm. is x = -(30) / (2·[-3]), or x = 5 time units.

The max height is thus h(5) = -3(5)^2 + 30(5) + 300 = 375 units.

Answer 2

Hello!

The answer is:

The maximum height reached by the projectile is 375 units.

Why?

To know what's the maximum height that the projectile reaches, we need to use the information about the given quadratic equation (parabola) to calculate the y-coordinate of the vertex.

The vertex of a parabola is located at the lowest or highest point depending on if the parabola opens upwards or downwards.

We can calculate the vertex of a parabola using the following equation:

`x_(vertex)=(-b)/(2a)`

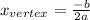
Then, after calculating the x-coordinate of the vertex, we need to substitute the x-coordinate value into the equation of the parabola to find the y-coordinate value or the highest point of the parabola.

We are given the parabola:

`h(x)=y=-3x^(2)+30x+300`

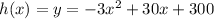
Where,

`a=-3\\b=30\\c=300\\`

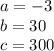
Now, calculating the vertex we have:

`x_(vertex)=(-b)/(2a)`

`x_(vertex)=(-30)/(2*(-3))=5`

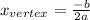
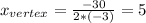
Then, calculating the y-coordinate value, we have:

`y_(vertex)=-3x^(2)+30x+300`

`y_(vertex)=-3*(5)^(2)+30*(5)+300`

`y_(vertex)=-3*25+150+300`

`y_(vertex)=-75+150+300`

`y=-75+150+300`

`y_(vertex)=375`

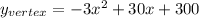
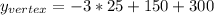
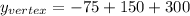
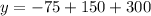
Hence, the y-coordinate value of the vertex is equal to 375, meaning that the maximum height reached by the projectile is 375 units.

Have a nice day!