Question

Chuck can afford a $490-per-month car payment, and he's interested in either

a convertible, which costs $28,700, or a sports car, which costs $29,200. If he
is being offered a 6-year car loan with an APR of 6%, compounded monthly,
which car can Chuck afford?
​

Answer 1

Chuck can afford both the convertible and sports car APEX

Explanation:

Answer 2

We can say that Chuck can afford both the cars.

Explanation:

The EMI formula is :

`(p*r*(1+r)^(n) )/((1+r)^(n)-1 )`

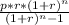
Case 1:

p = 28700

r = 6/12/100=0.005

n = 6*12=72

Putting the values in the above formula, we get:

`(28700*0.005*(1.005)^(72) )/((1.005)^(72)-1 )`

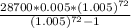
Monthly payment is = $475.67

Case 2:

p = 29200

r = 6/12/100=0.005

n = 6*12=72

Putting the values in the above formula, we get:

`(29200*0.005*(1.005)^(72) )/((1.005)^(72)-1 )`

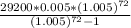
Monthly payment is = $483.96

We can see that in both the cases, the monthly payments or EMI's are less than $490.

Therefore, we can say that Chuck can afford both the cars.