Answer: C. - √2
Explanation:
Given requirements from the question
Find the exact value of sec 135°
Convert into common trigonometric expression
sec = secant
secx = 1 / cosx
Therefore, sec 135° = 1 / (cos 135°)
Find the reference angle
135° is quite a complicated angle, but it is possible to simplify it by finding its reference angle.
Since 135° is in the second quadrant, its reference angle will be
180° - 135° = 45°
However, we need to consider the positive and negative.
In a coordinate plane, the clue is (A S T C), which corresponds to the positive values in each quadrant. In the QI, "All" are positive. In the QII, sine is positive. In the QIII, the tangent is positive. In QIV, cosine is positive.
Therefore, when the value of cosine is in QII, it is negative.
The reference angle = - (1 / cos 45°)
Determine the final value
Given that the reference angle = - (1 / cos 45°)
cos 45° = 1 / √2
Therefore:
sec 135° = - (1 / cos 45°) = - (1 / (1 / √2)) =
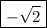
Hope this helps!! :)
Please let me know if you have any questions