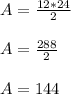Answer:
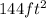
Explanation:
For this problem, we can use the formula for the area of a kite.
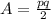
Where p and q are the diagonals.
Since line AE starts at the edge of the kite and ends at the center, we can multiply its value by 2 to find the value of the p diagonal.
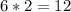
So diagonal p is 12ft.
Now we can find the value of the q diagonal, which will be adding BE and DE.
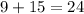
So diagonal q is 24ft.
Let's plug them into the area formula I mentioned earlier.