Question

What is the solution to this system of linear equations2x+3y=3 and 7x-3y24

Answer 1

The correct answer is

x = 3 and y = -1

Explanation:

It is given two system of equation

2x + 3y = 3 and 7x - 3y = 24

To find the solution

Let 2x + 3y = 3 ------(1)

7x - 3y = 24 (2)

eq(1) + eq (2) ⇒

9x + 0 = 27

x = 27/9 = 3

eq(1) ⇒

2x + 3y = 3

2*3 + 3y = 3

6 + y = 3

y = 3 6 = -3

y = -3/3 = -1

Therefore the solution of this system of equation is (3, -1)

Answer 2

For this case we have a system of two equations with two unknowns:

`2x + 3y = 3\\7x-3y = 24`

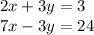
We follow the steps below:

We add the equations:

`9x = 27`

We divide between 9 on both sides of the equation:

`x = \frac {27} {9}\\x = 3`

We substitute the value of "x" in the first equation and find the value of y:

`2 (3) + 3y = 3\\6 + 3y = 3\\3y = 3-6\\3y = -3\\y = \frac {-3} {3}\\y = -1`

Thus, the solution of the system is: (3, -1)

Answer:

(3, -1)