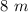Question

The sum of the areas of two circles is 80 pie square meters. Find the length of a radius of each circle if one of them is twice as long as the others

Answer 1

The radius of the circles are
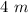`4\ m` and
`8\ m`

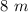
Explanation:

Let

x-----> the radius of larger circle

y----> the radius of smaller circle

we know that

`\pi x^(2) +\pi y^(2)=80\pi`

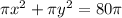
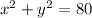`x^(2) +y^(2)=80` -----> equation A

Remember that

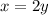`x=2y` -----> equation B

substitute equation B in equation A and solve for y

`(2y)^(2) +y^(2)=80`

`4y^(2) +y^(2)=80`

`5y^(2)=80`

`y^(2)=16`

`y=4\ m`

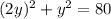
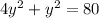
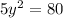
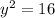
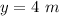
Find the value of x

`x=2y`

`x=2(4)=8\ m`

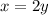
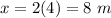
therefore

The radius of the circles are
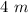`4\ m` and
`8\ m`