Question

What does the equation y = x2 - 6x + 5 become after completing the square?

Answer 1

Answer: Option B

Explanation:

Given the quadratic equation
`y=x^2-6x+5`:

You know that:

`((b)/(2))^2=((6)/(2))^2=3^2`

Group the variable "x" inside a parentheses:

`y=(x^2-6x)+`

Then, now you need to add 3² inside the parentheses and subtract 3² outside of the parentheses. Thenrefore, rewriting, you get:

`y=(x^2-6x+3^2)+(5-3^2)\\y=(x-3)^2-4`

This matches with the option B.

Answer 2

Hello!

The answer is:

The answer is: C.

`y=(x-3)^(2)-4`

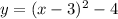
Why?

To answer this question, we need to remember the completing square process.

We can complete the square in the following way:

- Make the function equal to 0.

- Isolate the constant number (c).

- Find the number that completes the square using the following formula:

`((b)/(2))^(2)`

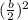
- Add the number that completes the square to both sides of the equation.

- Factorize the trinomial on one of the sides of the equation, and simplify the other side.

So, We are given the equation:

`y=x^(2) -6x+5`

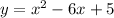
- Making it equal to 0, we have:

`0=x^(2) -6x+5`

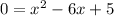
- Isolating the constant, we have:

`x^(2) -6x=-5`

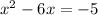
- Finding the number that completes the square:

`((b)/(2))^(2)=((-6)/(2))^(2)=(-3)^(2)=9`

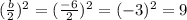
- Adding it to both sides of the equation:

`x^(2) -6x+9=-5+9`

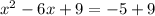
- Factoring and simplifying, we have:

`x^(2) -6x+9=-5+9`

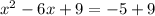
We need to find two numbers which product gives as result "9" and its algebraic sum gives as result "-6", this numbers is "-3", then, factoring, we have:

`(x-3)^(2)=4`

`(x-3)^(2)-4=0`

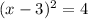
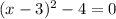
Then, the equation after completing the square will be:

`y=(x-3)^(2)-4`

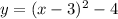
Hence, the answer is:

C.
`y=(x-3)^(2)-4`

Have a nice day!