Hello!
The answer is:
D. The parabola intercepts the x-axis in two points.
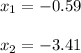
Why?
To find the parabola intercepts, we need to use the quadratic formula. The parabola intercepts with the x-axis, are also called roots or zeroes.
The quadratic formula states that:

We are given the parabola:
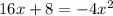
Which is also equal to:

Where,

Then, substituting into the quadratic formula to find the roots of the parabola, we have:

Hence,the parabola intercepts the x-axis in two points.
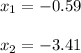
Have a nice day!