Answer:
The value of most expensive car he can afford is $ 22913.757.
Explanation:
Since, the periodic payment of a loan is,
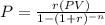
Where, P.V. is the presents value of the loan,
r is the rate per period,
n is the number of periods,
Here, Monthly payment, P = $ 330,
⇒ The loan is compound monthly,
Thus, if the time = 6 years,
The number of periods, n = 6 × 12 = 72 months, ( 1 year = 12 months ),
Also, the A.P.R = 1.2 % = 0.012
So, the rate per periods,
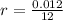
By substituting the values,
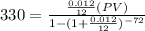
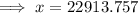
Hence, the value of most expensive car he can afford is $ 22913.757.