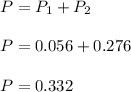Question

Suppose that 8% of the general population has a disease and that the test for the diesease is accurate 70% of the time. What is the probability of testing positive for the disease

Answer 1

P = 0.332

Explanation:

The probability of having the disease is 0.08

The probability that the test predicts with accuracy is 0.7.

We need to find the probability that the test positive for the disease.

Several cases may occur.

Case 1.

You have the disease and the test predicts it accurately

`P_1 = 0.08(0.7) = 0.056`

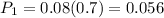
Case 2

You do not have the disease and the test predicts that you have it

`P_2 = 0.92(0.3) = 0.276`

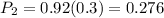
Then the probability that the test predicts that you have the disease is the union of both probabilities P1 and P2

`P = P_1 + P_2\\\\P = 0.056 + 0.276\\\\P = 0.332`