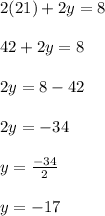Question

Solve the systems of equations 2x+2y+6z=8 5x+6y+5z =3 5x+6y+3z=3

Answer 1

`x=21\\y=-17\\z=0`

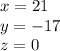
Explanation:

Multiply the second equation by -1:

`(-1)5x+6y+5z=3(-1)\\-5x-6y-5z=-3`

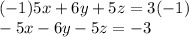
Add this equation and the third equation and solve for "z":

`\left \{ {{-5x-6y-5z=-3} \atop {5x+6y+3z=3}} \right.\\.........................\\-2z=0\\z=0`

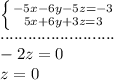
Substitute
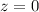`z=0` into two original equations:

`2x+2y+6(0)=8`

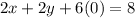
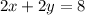`2x+2y=8` [Equation A]

`5x+6y+5(0)=3`

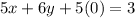
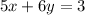`5x+6y=3` [Equation B]

Multiply the Equation A by -3, add both equations and then solve for "x":

`\left \{ {{-6x-6y=-24} \atop {5x+6y=3}} \right.\\.....................\\-x=-21\\x=21`

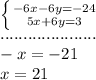
Substitute
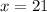`x=21` into the Equation A or the Equation B and solve for "y":

`2(21)+2y=8\\\\42+2y=8\\\\2y=8-42\\\\2y=-34\\\\y=(-34)/(2)\\\\y=-17`