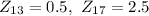Answer: Last option
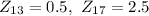
Explanation:
The z-scores give us information about how many standard deviations from the mean the data are. This difference can be negative, if the data are n deviations to the left of the mean, or it can be positive if the data are n deviations to the right of the mean.
To calculate the Z scores, we calculate the difference between the value of the data and the mean and then divide this difference by the standard deviation.
so
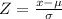 .
.
Where x is the value of the data, μ is the mean and σ is the standard deviation
In this case :
μ = 12 $/h
 = 2 $/h
= 2 $/h
We need to calculate the Z-scores for
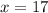 and
and
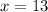
Then for
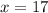 :
:
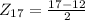 .
.
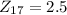
Then for
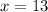 :
:
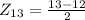 .
.
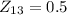
Therefore the answer is: