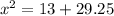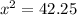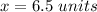Question

The area of the square adjacent to two sides of a right triangle are 29.25 square units and 13 units 30 POINTS

Answer 1

6.5 units

Explanation:

Answer 2

`x=6.5\ units`

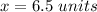
Explanation:

step 1

Find the length side of the smaller square

The area of the square is equal to

`A=a^(2)`

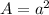
so

`a^(2)=13`

`a=√(13)\ units`

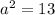
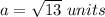
step 2

Find the length side of the larger square

The area of the square is equal to

`A=b^(2)`

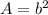
so

`b^(2)=29.25`

`b=√(29.25)\ units`

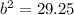
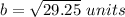
step 3

Find the value of x

Applying the Pythagoras Theorem

`x^(2) =a^(2)+b^(2)`

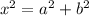
substitute the values

`x^(2) =13+29.25`

`x^(2) =42.25`

`x=6.5\ units`