Question

How many times does the graph of the function below intersect or touch the x axis? y=-3x^2+x+4​

Answer 1

Answer: Two times.

Explanation:

The graph touches the x-axis when the value of "y" is zero.

Then, substitute
`y=0` into the function:

`0=-3x^2+x+4`

Use the Quadratic formula to solve for "x":

`x=(-b\±√(b^2-4ac))/(2a)`

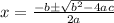
You can identify that:

`a=-3\\b=1\\c=4`

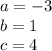
Then, you can substitute values into the Quadratic formula
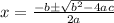`x=(-b\±√(b^2-4ac))/(2a)`, so you get:

`x=(-1\±√(1^2-4(-3)(4)))/(2(-3))\\\\x_1=(4)/(3)\\\\x_2=-1`

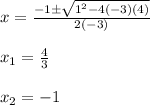
Therefore, the graph of this function touches the x-axis two times.