Answer:
i. BC
ii. |AD|=|7-2|=5
Explanation:
ABC has the points A(1, 7), B(-2, 2), and C(4, 2).
We use the distance formula to obtain
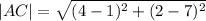
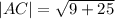
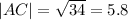

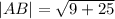
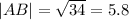
Using the absolute value method
|BC|=|4--2|=6
The longest side is BC
We use the absolute value method to find the length of AD
|AD|=|7-2|=5