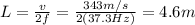Question

A nylon guitar string is fixed between two lab posts 2.00 m apart. The string has a linear mass density of μ=7.20 g/m\mu=7.20~\text{g/m}μ=7.20 g/m and is placed under a tension of 160.00 N. The string is placed next to a tube, open at both ends, of length L. The string is plucked and the tube resonates at the n=1 mode. The speed of sound is 343 m/s. What is the length of the tube?

Answer 1

The length of the tube is 4.00 meters.

Step-by-step explanation:

To find the length of the tube, we need to consider the harmonics of the vibrating string and the resonant frequencies of the tube. In the n=1 mode, the length of the tube will be half of the wavelength of the sound produced. The formula for the wavelength is given by:

λ = 2L/n

where λ is the wavelength, L is the length of the tube, and n is the mode of resonance. In this case, n=1. So, substituting the given values into the formula, we have:

λ = 2(2.00 m)/1 = 4.00 m

Therefore, the length of the tube is 4.00 meters.

Answer 2

4.6 m

Step-by-step explanation:

First of all, we can find the frequency of the wave in the string with the formula:

`f=(1)/(2L)\sqrt{(T)/(\mu)}`

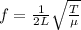
where we have

L = 2.00 m is the length of the string

T = 160.00 N is the tension

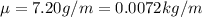`\mu =7.20 g/m = 0.0072 kg/m` is the mass linear density

Solving the equation,

`f=(1)/(2(2.00 m))\sqrt{(160.00 N)/(0.0072 kg/m)}=37.3 Hz`

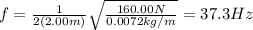
The frequency of the wave in the string is transmitted into the tube, which oscillates resonating at same frequency.

The n=1 mode (fundamental frequency) of an open-open tube is given by

`f=(v)/(2L)`

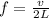
where

v = 343 m/s is the speed of sound

Using f = 37.3 Hz and re-arranging the equation, we find L, the length of the tube:

`L=(v)/(2f)=(343 m/s)/(2(37.3 Hz))=4.6 m`