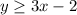Question

What is the answer for this? please help!

Answer 1

For this case, the first thing to do is find the equation of the line, of the form
`y = mx + b`

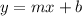
Where:

m: It's the slope

b: It is the cutoff point with the y axis

`m=(y2-y1)/(x2-x1)\\m=(-2-1)/(0-1)\\m=(-3)/(-1)\\m=3`

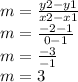
Thus, the equation is:

`y = 3x + b`

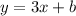
Replace any of the points to find b:

`1 = 3 (1) + b\\1 = 3 + b\\b = 1-3\\b = -2`

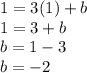
Finally, the equation is:

`y = 3x-2`

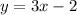
Now, we must determine the sign of inequality.

We have two possible options, in each one we will substitute a point in the region to know if it is fulfilled:

• 
  `y\geq3x-2\\Point\ (0,0)\\0\geq3 (0) -2\\0\geq- 2`

Is fulfilled.

• 
  `y \leq3x-2\\Point\ (0,0)\\0 \leq0-2\\0\leq- 2`

It is not fulfilled Therefore, the shaded region corresponds to:

`y\geq3x-2`

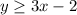
Answer:

`y\geq3x-2`