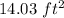Question

Hw 27 area of composites

Answer 1

We must find the area of ​​each of the figures shown:

Question 1:

For this case, we have by definition, that the area of ​​a rectangle is given by:

`A = a * b`

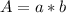
Where a and b are the sides of the rectangle.

The area of ​​the first figure is given by the sum of the areas of three rectangles, then:

`A_ {1} = 6 * 3 + 5 * 3 + 6 * 3\\A_ {1} = 18 + 15 + 18\\A_ {1} =51`

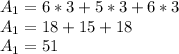
Thus, the area of ​​the first figure is 51 square centimeters.

Answer:

`51 \ cm ^ 2`

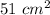
Question 2:

For this case, we have that by definition, the area of ​​a rectangle is given by:

`A = a * b`

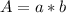
Where a and b are the sides.

The area of ​​a square is given by:

`A = l ^ 2`

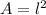
Where l is the side of the square

The area of ​​the figure is given by the sum of the area of ​​a rectangle and a square:

`A_(2) = 9 * 2 + 3 ^ 3\\A_(2) = 18 + 9\\A_(2) = 27`

Thus, the area of ​​the second figure is 27 square inches.

Answer:

`27 \ in ^ 2`

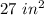
Question 3:

For this case, we have that by definition, the area of ​​a rectangle is given by:

`A = a * b`

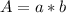
Where a and b are the sides of the rectangle.

While the area of ​​a circle is given by

`A = \pi * r ^ 2`

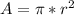
Where r is the radius of the circle.

The area of ​​the third figure is found under a subtraction (the area of ​​a rectangle minus the area of ​​the middle of a circle)

So:

`A_ {3} = 50 * 30- \frac {\pi * 15 ^ 2} {2}\\A_ {3} = 1500-112.5 \pi\\A _(3) = 1500-353.43\\A _(3) = 1146.6`

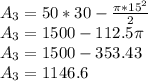
Thus, the area of ​​the third figure is 1146.6 square feet.

Answer

`1146.6 \ ft ^ 2`

Question 4:

For this case, the area of ​​the fourth figure is given by the area of ​​a rectangle plus the sum of two halves of areas of a circle.

So:

`A_ {4} = 30 * 15 + \frac {\pi * (7.5) ^ 2} {2} + \frac {\pi * (7.5) ^ 2} {2}\\A_ {4} = 450 + \pi * (7.5) ^ 2\\A_(4) = 450 + 56.25\\A_ {4} = 506.25`

Thus, the area of ​​the fourth figure is 506.25 square centimeters.

Answer:

`506.25 \ cm ^ 2`

Question 5:

The area of ​​the last figure is given by the sum of the area of ​​a triangle plus the area of ​​half a circle.

So:

`A_ {5} = \frac {3 * 7} {2} + \frac {\pi * (1.5) ^ 2} {2}\\A_(5) = 10.5 + 3.53\\A_(5) = 14.03`

Thus, the area of ​​the fifth figure is given by 14.03 square feet.

Answer:

`14.03 \ ft ^ 2`