Question

Van guessed on all 8 questions of a multiple-choice quiz. Each question has 4 answer choices. What is the probability that he got exactly 1 question correct? Round the answer to the nearest thousandth.

0.033
0.267
0.733
0.801

Answer 1

B. 0.267

Explanation:

Answer 2

0.267

Explanation:

This can be solved using the binomial probability formula which is:

`P(success)=nCk*p^(k)(1-p)^(n-k)`

Where

n is total number of trials (here, the total number of questions is 8, so n = 8)

k is the number of attempts we are looking for (here, we want to find probability of 1 question correct, so k = 1)

p is the probability of success (here, success is getting a questions right. Since there are 4 choices and 1 is right, probability of right = 1/4)

Plugging all the info into the formula we get:

`P(success)=nCk*p^(k)(1-p)^(n-k)\\P(1QuestionRight)=8C1*((1)/(4))^(1)(1-(1)/(4))^(8-1)\\P(1QuestionRight)=(8!)/((8-1)!*1!)((1)/(4))((3)/(4))^7\\P(1QuestionRight)=(8!)/(7!*1!)((1)/(4))((3)/(4))^7\\P(1QuestionRight)=8((1)/(4))((3)/(4))^7\\=0.267`

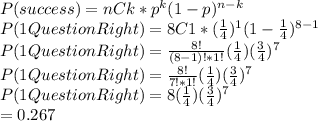
Second choice is right.