Aron flips a penny 9 times. Which expression represents the probability of getting exactly 3 heads?

Question

asked Oct 17, 2020 233k views

2 Answers

LastFreeNickname · Answer 1 · 2020-10-21T06:30:07+0000

Answer:

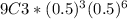
9C3*(0.5)^3(0.5)^6

Explanation:

The binomial probability formula shown has variables which represents:

n is the total number of trials (here, we flip penny 9 times, hence n = 9)

k is the number we want to find (here, we want the probability of 3 heads, so k = 3)

p is the probability of success (here, success means getting heads. So, in a coin flip the probability of heads is always 1/2, so p = 1/2)

Putting all the info into the equation and using formula for nCk, we get:

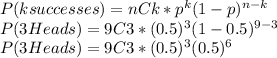
$P(k successes)=nCk*p^(k)(1-p)^(n-k)\\P(3Heads)=9C3*(0.5)^3(1-0.5)^(9-3)\\P(3Heads)=9C3*(0.5)^3(0.5)^6$

The first expression shown in the answer choices is right.