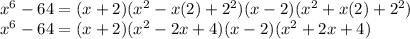Explanation:
Part A:
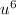 can be written as the square of u³, or
can be written as the square of u³, or
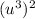 . Similarly,
. Similarly,
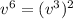 . Hence, we can write this as a difference of two squares by writing it as
. Hence, we can write this as a difference of two squares by writing it as

Part B:
Difference of Two Squares
We can first factor a difference of two squares a² - b² into (a+b)(a-b). Here, a would be u³ and b would be v³.
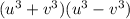
Sum and Difference of Two Cubes
We can factor this further by the use of two special formulas to factor a sum of two cubes and a difference of two cubes. These formulas are as follows:
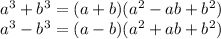
Since u³ + v³ is a sum of two cubes, let's rewrite it.

Since u³ - v³ is a difference of two cubes, we can rewrite it as well.
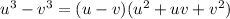
Now, let's multiply them together again to get the final factored form.
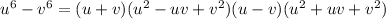
Part C:
If we want to factor
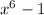 completely, we can just see that x to the sixth power is just
completely, we can just see that x to the sixth power is just
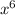 and 1 to the sixth power is just 1. Hence, x can substitute for u and 1 can substitute for v.
and 1 to the sixth power is just 1. Hence, x can substitute for u and 1 can substitute for v.
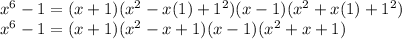
We can repeat this for
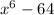 , as 64 is just 2 to the sixth power.
, as 64 is just 2 to the sixth power.