Question

Find the surface area and volume of cone. A = rs + r2 V = 1/3r2 h A cone's slant height (s) is 14 cm and its radius is 4.5 cm. Surface area (to the nearest tenth) = cm2 Volume (to the nearest tenth) = cm3

Answer 1

Surface area
`= 261.405 cm^2\\`

Volume of the cone
`= 177.19 cm^3\\`

Explanation:

Slant height of cone
`= (r + √(r^2 + h^2)) \\`

Height of the cone will be derived from this slant height

`14 = 4.5 + √(4.5^2 + h^2) \\9.5 = √(4.5^2 + h^2)\\90.25 = 20.25 + h^2\\h = 8.36\\`

Surface Area of Cone

`= \pi r (r + l)\\= (3.14) (4.5) (4.5 + 14)\\= 261.405`

Volume of the cone

`= (1)/(3) \pi r^2h\\= (1)/(3) (3.14)(4.5^2) (8.36)\\= 177.19 cm^3\\`

Answer 2

Surface area =
`261.6cm^2`

Volume =
`281.2cm^3`

Explanation:

To find the surface area of our cone, we are using the formula for the surface area of a cone:

`A=\pir(r+√(h^2+r^2) )`

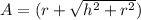
where

`A` is the surface area

`r` is the radius

`h` is the height

Notice that the height, radius, and slant height make a right triangle, so to find the height,
`h`, we can use the Pythagorean theorem:

`s^2=r^2+h^2`

`14^2=4.5^2+h^2`

`196=20.25+h^2`

`h^2=196-20.25`

`h^2=175.75`

`h=√(175.75)`

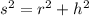
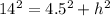
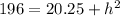
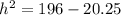
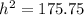
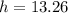`h=13.26` cm

We have all we need now to find the surface area of our cone:

`A=\pir(r+√(h^2+r^2) )`

`A=\pi(4.5)(4.5+√(13.26^2+4.5^2) )`

`A=261.6cm^2`

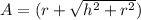
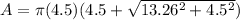
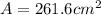
Now, to find the volume of our cone, we are using the formula for the volume of a cone:

`V=(\pi r^2h)/(3)`

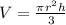
where

`V` is the volume

`r` is the radius

`h` is the height

Replacing values

`V=(\pi (4.5^2)(13.26))/(3)`

`V=281.2cm^3`

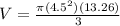
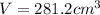
We can conclude that the surface area of our cone is 261.6 square centimeters and its volume is 281.2 cubic centimeters.