Answer:
Center: (2,-1)
Radius: 4 units
Explanation:
Equation of the circle in standard form is:
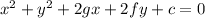
The radius of this circle is located at (-g, -f) and its radius is equal to:
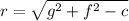
The given equation of circle is:
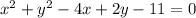
Re-writing this equation in a form similar to the standard equation:
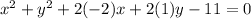
Comparing this equation with standard equation we can say:
g= -2
f = 1
c = -11
So, the center of the circle will be located at (-g, -f) = (2, -1)
And the radius will be =
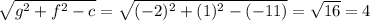
Thus the radius of the given circle is 4 units.