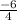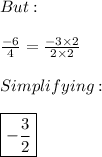Question

Explain the steps needed to determine the value of the expression shown below. Be sure to provide the correct value of the expression in your explanation.

Answer 1

Let's write the expression:

`((1)/(2))/(-(2)/(5))+\left(-(1)/(4)\right)`

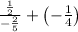
So we have two terms here. The first term is a complex fraction because both the numerator and denominator contain fractions. To simplify this, let's flip the denominator to find its inverse because by dividing one number by another you get the same result as multiplying the first number by the inverse of the second. So:

`((1)/(2))/(-(2)/(5))=(1)/(2)\left(-(5)/(2)\right)`

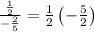
Next, we multiply
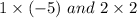`1* (-5) \ and \ 2* 2` the result of our first term is:

`(1)/(2)\left(-(5)/(2)\right)=-(5)/(4)`

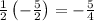
Now, we need to solve this:

`-(5)/(4)+\left(-(1)/(4)\right)`

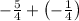
So this is the same as:

`-(5)/(4)-(1)/(4)`

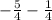
Since we have the same denominator in both terms, we can set a fraction with the same denominator and adding the numerators:

`(-5-1)/(4)`

Finally:

`(-6)/(4)`

`But: \\ \\ (-6)/(4)=(-3* 2)/(2* 2) \\ \\ Simplifying: \\ \\ \boxed{-(3)/(2)}`