Question

The figure is made up of a rectangle and parallelogram. What is the area of this figure ?

Do not round any side lengths.

Answer 1

26

explanation:

I took the quiz

Answer 2

26 square units

Explanation:

Let's label the vertices of our figure first:

A = (-10, 2)

B = (-4, 2)

C = (-2, -4)

D = (1, -3)

E = (-1, 3)

F = (-7, 3)

We are drawing the line segment AE to divide our figure in parallelogram ABEF and rectangle BCDE.

The are of the figure will be the area of parallelogram ABEF plus the area of rectangle BCDE.

To find the area of ABEF, we are using the formula for the area of a parallelogram:

`A=bh`

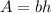
Where

`A` is the area

`b` is the base

`h` is the height

The base of our parallelogram is the side AB. remember that the height of a parallelogram is the distance between two opposite sides; the sides of our parallelogram are AB and DF, so its height is
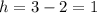`h=3-2=1`. Now to find the length of the base, we are using the distance formula:

distance formula:

`d=\sqrt{(x_2-x_1)^(2) +(y_2-y_1)^(2)}`

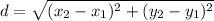
where

`(x_1,y_1)` are the coordinates of the first point

`(x_2,y_2)` are the coordinates of the second point

Replacing values

`d=\sqrt{[-4-(-10)]^(2) +(2-2)^(2)}`

`d=\sqrt{(-4+10)^(2) +(0)^(2)}[/tex</p><p>[tex]d=√((-6)^2)`

`d=√(36)`

`d=6`

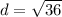
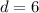
We now have all we need to find the area of ABEF:

`A=bh`

`A=(6)(1)`

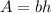
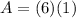
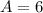`A=6` square units

Now, to the find the area of BCDE, we are using the formula for the area of a rectangle:

`A=wl`

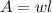
where

`A` is the area

`w` is the width

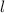`l` is the length

The width of BCDE is BE and its length is BC. Using the distance formula again:

- For BE

`d=\sqrt{[-1-(-4)]^(2) +(3-2)^(2)}`

`d=\sqrt{(-1+4)^(2) +(1)^(2)}`

`d=\sqrt{(3)^(2) +1}`

`d=√(9 +1)`

`d=√(10)`

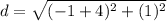
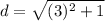
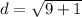
- For BC

`d=\sqrt{[-2-(-4)]^(2) +(-4-2)^(2)}`

`d=\sqrt{(-2+4)^(2) +(-6)^(2)}`

`d=\sqrt{(2)^(2)+36}`

`d=√(4+36)`

`d=√(40)`

`d=2√(10)`

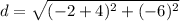
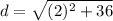
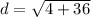
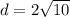
We now have all we need to find the area of BCDE:

`A=wl`

`A=(√(10) )(2√(10) )`

`A=2(√(10))^2`

`A=2(10)`

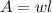
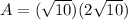
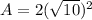
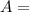`A=` square units.

All we have left is add the areas of ABEF and BCDE:

Area of the figure = ABEF + BCDE

Area of the figure = 6 + 20

Area of the figure = 26 square units