Question

Write an equation in slope-intercept form of the line perpendicular to y = 3x + 4 that passes through the point (3, 4).

A) y = 3x - 5
B) y = 3x + 5
C) y = 1 3 x + 5
D) y = - 1 3 x + 5

Answer 1

(D) y= -1/3 x +5

Explanation:

Perpendicular lines have gradients that multiply to give -1

Equation given, y=3x+4

gradient m₁=3

Finding m₂ we know m₁×m₂= -1

Thus m₁×m₂=-1 ⇒ 3×m₂=-1

m₂= -1/3

Equation of new line passing through points (3,4) with gradient m₂=-1/3 will be;

Δy/Δx =m₂

(y-4)/(x-3) = - 1/3

3(y-4)= -1(x-3)

3y-12= -x+3

3y=-x+3+12

3y/3= -x/3 + 15/3

y= -1/3 x +5

Answer 2

The correct answer option is D.
`y= -(1)/(3) x+5`.

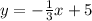Explanation:

We are to find the equation of a line which is perpendicular to the following line and passes through the point (3, 4):

`y = 3x + 4`

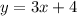
We know that an equation perpendicular to another equation has a slope which is the negative reciprocal of the first equation.

So our required slope is
`-(1)/(3)`

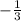
Finding the y-intercept:

`y=mx+c`

`4=-(1)/(3)(3)+c`

`c=5`

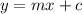
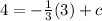
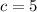
Therefore, the equation of the line perpendicular to
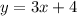`y = 3x + 4` and passing through the point (3, 4) is
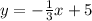`y= -(1)/(3) x+5`.