Because the curve crosses the
 -axis at
-axis at
 , we know the point (2, 0) lies on the curve, so that
, we know the point (2, 0) lies on the curve, so that

Tangents to the curve have slope
 :
:
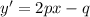
and at the point (1, -2), the slope is 1, so that

This also tells us the point (1, -2) is on the curve, so that
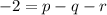
Solve for
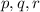 ; you should get
; you should get
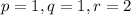
so the equation of the curve is
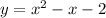
Factorizing this yields
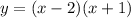
which means
 is a root and the curve intersects the
is a root and the curve intersects the
 -axis at the point (-1, 0).
-axis at the point (-1, 0).