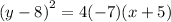Question

Write the equation of a parabola with vertex (-5,8) and directrix x=2. Show all of your work and put your equation in graphing/vertex form

if anyone can help that'd be amazing :)

Answer 1

`{(y - 8)}^(2) = - 28(x + 5)`

Step-by-step explanation

The equation of a parabola whose axis of symmetry is parallel to the x-axis is given by;

`{(y - k)}^(2) = 4p(x - h)`

where (h ,k)=(-5,8) is the vertex and p is the focal length.

The focal length is the distance from the focus to the vertex.

This is equal to the distance from the vertex to the directrix.

p=2--5=7

But because the parabola opens in the negative direction of the x-axis, its equation becomes,

`{(y - 8)}^(2) = 4( - 7)(x + 5)`

`{(y - 8)}^(2) = - 28(x + 5)`