Question

Here is rectangle QRST.

What is QR?
What is RS? And what is the perimeter of rectangle QRST?

Answer in units

Answer 1

Answers with step-by-step explanation:

We are given the following coordinates of the rectangle QRST:

Q (-3, 0)

R (0, 4)

S (8, -2)

T (5, -6)

QR =
`\sqrt { ( 4 - 0 ) ^ 2 + ( 0 - ( - 3 ) ) ^ 2 } = \sqrt { 1 6 + 9 } = \sqrt { 2 5 }` = 5 units

RS =
`\sqrt { ( 4 - ( - 2 ) ) ^ 2 + ( 0 - 8 ) ^ 2} = \sqrt { 3 6 + 6 4 } =√(100)` = 10 units

Perimeter of QRST =
`2 (QR+RS) = 2(5+10)` = 30 units

Answer 2

QR = 5 units

RS = 10 units

Perimeter of QRST = 30 units

Explanation:

The perimeter of a rectangle is given by the formula:

`p=2(l+w)`

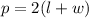
where

`p` is the perimeter of the rectangle

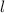`l` is the length of the rectangle

`w` is the width of the rectangle

Now, to find the width, QR, and the length, RS, of the rectangle, we are using the distance formula:

`d=\sqrt{(x_2-x_1)^(2)+(y_2-y_1)^(2)}`

where

`d` is the distance

`(x_1,y_1)` are the coordinates of the first point

`(x_2,y_2)` are the coordinates of the second point

- For QR:

The first point of QR is Q(-3, 0) and the second is R(0, 4), so
`x_1=-3`,
`y_1=0`,
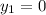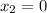`x_2=0`, and
`y_2=4`.

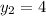Replacing values

`d=\sqrt{(x_2-x_1)^(2)+(y_2-y_1)^(2)}`

`d=\sqrt{(0-(-3))^(2)+(4-0)^(2)}`

`d=\sqrt{(0+3)^(2)+(4)^(2)}`

`d=\sqrt{3^(2) +4^(2)}`

`d=√(9+16)`

`d=√(25)`

`d=5`

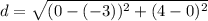
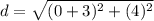
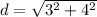
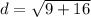
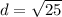
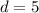
- For RS

The first point of RS is R(0, 4) and the second is S(8, -2), so
`x_1=0`,
`y_1=4`,
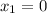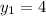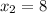`x_2=8`, and
`y_2=-2`.

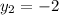Replacing values

`d=\sqrt{(8-0)^(2)+(-2-4)^(2)}`

`d=\sqrt{(8)^(2)+(-6)^(2)}`

`d=√(64+36)`

`d=√(100)`

`d=10`

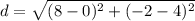
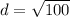
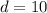
Now that we know that the width QR is 5 units and the length RS is 10 units, we can find the perimeter of our rectangle:

`p=2(l+w)`

`p=2(RS+QR)`

`p=2(10+5)`

`p=2(15)`

`p=30`

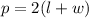
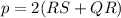
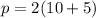
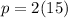
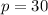
We can conclude that QR = 5 units, RS = 10 units, and the perimeter of rectangle QRST is 30 units.