Question

What is the answer for this?

Answer 1

5/12 and -11/12

Explanation:

We need to solve the equation using quadratic formula but before that, there should be only one constant term so,

`x^2+(1x)/(2) + (1)/(16)= (4)/(9)\\\\x^2+(1x)/(2) = (4)/(9) -  (1)/(16)\\\\x^2+(1x)/(2) = (4*16 - 1*9)/(144)\\\\x^2+(1x)/(2) = (55)/(144)\\\\x^2+(1x)/(2) -(55)/(144)= 0`

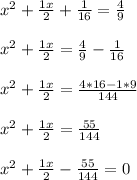
Now using quadratic formula to find the value of x

`x=(-b\pm√(b^2-4ac))/(2a)\\x=\frac{-(1)/(2)\pm\sqrt{((1)/(2))^2-4(1)((-55)/(144))}}{2(1)}\\\\x=\frac{-(1)/(2)\pm\sqrt{(1)/(4)+((55)/(36))}}{2}\\\x=\frac{-(1)/(2)\pm\sqrt{(9+55)/(36)}}{2}\\\x=\frac{-(1)/(2)\pm\sqrt{(64)/(36)}}{2}\\\\x=\frac{-(1)/(2)\pm{(8)/(6)}}{2}\\\\so\,\,x=(-(1)/(2)+(8)/(6))/(2)\,\, and\,\, x=(-(1)/(2)-(8)/(6))/(2)\\ \\`

Solving these equations,

`x= (-3+8)/(12) \,\, and \,\, x=(-3-8)/(12)\\\\x= (5)/(12) \,\, and \,\, x=(-11)/(12)`

So, x= 5/12 and x= -11/12