Answer:
5/12 and -11/12
Explanation:
We need to solve the equation using quadratic formula but before that, there should be only one constant term so,
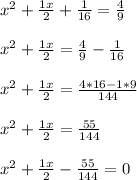
Now using quadratic formula to find the value of x

Solving these equations,
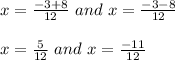
So, x= 5/12 and x= -11/12