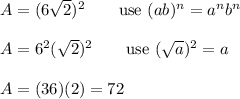1 Answer

Decent Dabbler · Answer 1 · 2020-09-10T10:32:45+0000

Answer:

D) 72

Explanation:

A distance between a center of a circle and other point on the circle is equal to a length of a radius.

The formula of a distance between two points:

d=√((x_2-x_1)^2+(y_2-y_1)^2)

We have the center (2, 5) and the point on the circle (5, 2). Substitute:

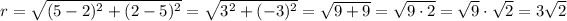
$r=√((5-2)^2+(2-5)^2)=√(3^2+(-3)^2)=√(9+9)=√(9\cdot2)=\sqrt9\cdot\sqrt2=3\sqrt2$

The length of the side of the square is equal to twice the length of the radius of the circle inscribed in the square.

Therefore:

a - length of the side of the square

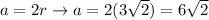
$a=2r\to a=2(3\sqrt2)=6\sqrt2$

The formula of an area of a square:

A=a^2

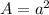
Substitute:

$A=(6\sqrt2)^2\qquad\text{use}\ (ab)^n=a^nb^n\\\\A=6^2(\sqrt2)^2\qquad\text{use}\ (√(a))^2=a\\\\A=(36)(2)=72$